Menyajikan Hubungan Antarhimpunan Dengan Diagram Venn
Pengantar
Seperti yang diketahui, cara menyajikan himpunan bisa dilakukan dengan menggunakan kata-kata atau deskripsi, dengan notasi pembentuk himpunan, dan dengan mendaftar anggota-anggotanya. Selain itu, ada satu cara lainnya untuk menyajikan himpunan yaitu dengan menggunakan diagram Venn. Kenapa dinamakan diagram Venn? Karena diagram ini pertama kali diperkenalkan oleh matematikawan Inggris yaitu John Venn (1834 - 1923). Petunjuk dalam membuat diagram Venn antara lain adalah :
- Himpunan semesta (S) digambarkan sebagai persegi panjang dan huruf S diletakkan di sudut kiri atas. Selain huruf S ada juga yang menggunakan huruf U.
- Setiap himpunan yang ada dalam himpunan semesta ditunjukkan oleh kurva tertutup sederhana.
- Setiap anggota himpunan ditunjukkan dengan titik.
- Bila anggota suatu himpunan mempunyai banyak anggota, maka anggota-anggotanya tidak perlu dituliskan.
Contoh diagram Venn ditunjukkan pada gambar berikut.
Hubungan Antarhimpunan
Hubungan antarhimpunan dapat digambarkan dalam bentuk diagram Venn berikut.
1. Himpunan Bagian
Pada gambar (a) himpunan $A$ adalah himpunan bagian dari himpunan $B$ ($A\subset B$). Setiap anggota $A$ termasuk anggota $B$.
2. Himpunan yang Sama
Pada gambar (b) terlihat semua anggota himpunan $A$ menjadi anggota himpunan $B$, demikian juga sebaliknya. Hubungan antara $A$ dan $B$ disebut himpunan yang sama dan ditulis sebagai $A=B$.
3. Himpunan Saling Lepas
Pada gambar (c) himpunan $A$ dan $B$ dikatakan saling lepas karena himpunan $A$ dan $B$ tidak memiliki anggota persekutuan.
4. Himpunan Berpotongan
Pada gambar (d) himpunan $A$ dan $B$ dikatakan berpotongan karena $A$ dan $B$ memiliki anggota persekutuan dan masing-masing juga memiliki aggota yang bukan persekutuan.
Himpunan Ekuivalen
Untuk memahami himpunan yang ekuivalen, perhatikan uraian berikut.
Jika $y=x+1$ dengan $x$ anggota bilangan cacah ($C$) dan $y$ anggota himpunan bilangan asli ($N$), maka kita peroleh nilai seperti tabel berikut.
| $x$ | 0 | 1 | 2 | 3 | ... |
|---|---|---|---|---|---|
| $y$ | 1 | 2 | 3 | 4 | ... |
$C=\{0,1,2,3,\cdots\}$
$N=\{1,2,3,4,\cdots\}$
Hubungan $C$ dan $N$ dapat dilihat pada gambar berikut.
Perhatikan bahwa humpunan $C$ dan $N$ merupakan korespondensi satu-satu. Korespondensi satu-satu terjadi jika banyaknya anggota pada kedua himpunan sama. Sehingga hubungan $C$ dan $N$ adalah himpunan yang ekuivalen, dan ditulis $C\sim N$
Kesimpulan :
Dua himpunan A dan B dikatakan ekuivalen jika $n(A) = n(B)$ dan ditulis $A\sim B$
Contoh Soal dan Pembahasan
1. Diketahui :
$S=\{1,2,3,4,5,6,7,8,9,10\}$
$A=\{1,3,5,7\}$
$B=\{2,3,5,7,9\}$
Jika $S$ merupakan himpunan semesta, gambarlah diagram Venn dari himpunan-himpunan tersebut.
Jawab.
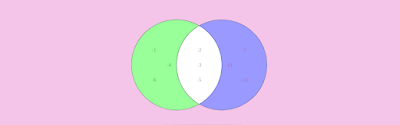
Pada diagram Venn tersebut, tampak bahwa $3, 5, \text{dan}\ 7$ merupakan anggota dari $A$ dan $B$.
2. Diketahui.
$S=\{0,1,2,3,\cdots,10\}$
$A=\{1,2,3,4\}$
$B=\{5,6,7,8\}$
$C=\{0,1,2,3\}$
$D=\{2,3,4\}$
$E=\{2,3,5,7\}$
$F=\{3,5,7\}$
Pertanyaan :
a. Tunjukkan dengan menggunakan diagram Venn setiap pasangan himpunan di atas.
b. Manakah pasangan himpunan yang saling lepas, berpotongan, dan himpunan bagian.
c. Adakah pasangan himpunan yang sama?
d. Adakah pasangan himpunan yang ekuivalen?
Jawab.
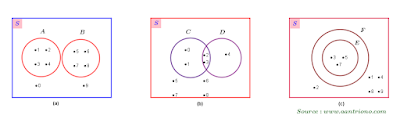
a.
b. Pada gambar tersebut (a), himpunan $A$ dan $B$ saling lepas.
Himpunan $C$ dan $D$ berpotongan dengan anggota-anggota persekutuan 2 dan 3.
Himpunan F merupakan himpunan bagian dari $E$.
c. Tidak ada
d. Ada, yaitu himpunan $A$ dan $B$ karena $n(A)=n(B)=4$
Penutup
Salah satu cara yang efektif dan efisien dalam menyajikan himpunan adalah dengan menggunakan diagram Venn, karena kita bisa menuliskan beberapa himpunan di dalamnya sekaligus mengekspresikan hubungan antara himpunan dalam sekelompok objek yang memiliki kesamaan nilai atau jumlah.
Demikian materi tentang menyajikan hubungan antarhimpunan dengan diagram Venn. Semoga bermanfaat. Terima kasih.
Traktir saya minum kopi dengan cara memberi donasi. klik icon panah di atas. Terima kasih.



Posting Komentar
image quote pre code