Bangun Ruang Sisi Lengkung
A. Kompetensi Dasar
3.7 Membuat generalisasi luas permukaan dan volume bangun ruang sisi lengkung (tabung, kerucut dan bola).
4.7 Menyelesaikan masalah kontekstual yang berkaitan dengan luas permukaan dan volume bangun ruang sisi lengkung (tabung, kerucut, dan bola) serta gabungan beberapa bangun ruang sisi lengkung.
3.7 Membuat generalisasi luas permukaan dan volume bangun ruang sisi lengkung (tabung, kerucut dan bola).
4.7 Menyelesaikan masalah kontekstual yang berkaitan dengan luas permukaan dan volume bangun ruang sisi lengkung (tabung, kerucut, dan bola) serta gabungan beberapa bangun ruang sisi lengkung.
B. Tujuan Pembelajaran (Materi Tabung)
Setelah mempelajari materi tabung ini, diharapkan dapat :
1. Menyebutkan unsur-unsur tabung
2. Menghitung luas alas, luas selimut, dan luas tutup tabung.
3. Menghitung volume tabung.
4. Menghitung unsur-unsur tabung jika volume tabung diketahui.
5. Menghitung perbandingan volume tabung karena perubahan ukuran
jari-jari.
6. Menghitung besar perubahan volume tabung, jika jari-jari berubah.
C. Materi
1. Unsur-unsur tabung
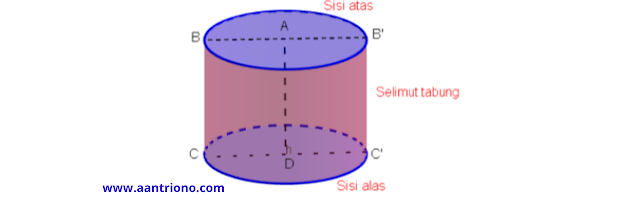
Tabung merupakan salah satu bangun ruang sisi lengkung. Tabung adalah bangun ruang sisi lengkung yang dibentuk oleh dua buah lingkaran identik yang sejajar dan sebuah persegi panjang yang mengelilingi kedua lingkaran tersebut.
Dari gambar tersebut kita peroleh :
1. Terdapat tiga sisi pada tabung, yaitu sisi alas, sisi tegak (berupa bidang lengkung)
dan sisi atas. Sisi alas dan sisi atas berbentuk lingkaran masing-masing
berpusat di A dan D. Sisi tegak sering disebut sebagai
selimut tabung.
2. Jarak alas dan tutup (atas)
disebut tinggi tabung. Tinggi tabung biasanya dinotasikan dengan
t.
3. Jari-jari lingkaran dari alas dan tutup adalah $\overline{CD}$ dan
$\overline{AB}$, sedangkan diameternya $BB'=2AB$, jari-jari tabung
dinotasikan dengan $r$, sedangkan diameter dinotasikan dengan $d$.
2. Jaring-jaring Tabung
Perhatikan gambar berikut!
3. Luas Permukaan Tabung
Untuk mencari luas permukaan tabung, kita bisa menggunakan luas
jaring-jaring tabung karena luas permukaan tabung sama dengan luas
jaring-jaring tabung. Luas permukaan tabung sering juga ditulis dengan
luas sisi tabung. Perhatikan kembali gambar jaring-jaring tabung di
atas.
1. Luas lingkaran alas = $\pi r^2$
2. Luas selimut tabung = luas persegi panjang = keliling alas x tinggi
tabung
= $2\pi r t$
3. Luas lingkaran tutup = $\pi r^2$
Jadi luas permukaan tabung = luas lingkaran alas + luas selimut tabung +
luas lingkaran tutup
$\begin{aligned}&= \pi r^2 +2\pi r t +\pi r^2\\&= 2\pi r^2 + 2\pi r t\\&= 2\pi r (r+t)\end{aligned}$
Contoh soal :
Sebuah tabung mempunyai tinggi $13$ cm dan jari-jari alasnya $7$ cm.
Tentukan luas sisi tabung.
Penyelesaian :
Luas sisi tabung
$\begin {aligned}&=2\pi r(r+t)\\&=2\times \frac{22}{7}\times
7\times (7+13)\\&=44\times 20\\&=880\end {aligned}$
Jadi luas sisi tabung adalah $880$ $cm^2$
4. Volume Tabung
Tabung memiliki alas berupa lingkaran maka volume tabung sama dengan luas
alas lingkaran dikalikan tinggi. Untuk setiap tabung berlaku rumus
berikut.
atau
$V = \frac{1}{4}\pi d^2 t$
Contoh soal :
1. Diketahui tabung dengan jari-jari $14$ cm dan tingginya $20$ cm.
Tentukan volume tabung.
2. Pada sebuah tempat minum berbentuk tabung, tertera volume $693$ ml.
Jika tinggi tabung $18$ cm, dengan anggapan tempat minum terisi penuh,
tentukan panjang diameternya dan luas sisi tempat minum tersebut.
Penyelesaian :
1. Volume tabung = $\pi r^2 t = \frac {22}{7}\times 14^2\times 20 =
12.320$
Jadi volume tabung adalah $12.320\ cm^3$
2. Volume tempat minum $693$ ml = $693$ $cm^3$
a. Volume tabung
$\begin {aligned}V&=\pi r^2 t\\693&=3,14\times r^2\times
18\\693&=56,52\
r^2\\r^2&=\frac{693}{56,52}\\r&=\sqrt{12,26}\\r&=3,5\end
{aligned}$
Karena $r=3,5$ cm, maka $d = 2\times 3,5$ cm = $7$ cm.
Jadi panjang diameter tempat air minum tersebut adalah $7$ cm.
b. Luas sisi tabung
$\begin {aligned}&=2\pi r(r+t)\\&=2\times \frac{22}{7}\times
3,5\times (3,5+18)\\&=473\end {aligned}$
Jadi luas sisi tabung adalah $473$ $cm^2$
Rumus-rumus penting
- Luas alas tabung = $\pi r^2$
- Luas selimut tabung = $2\pi r t$
- Luas tutup tabung = $\pi r^2$
- Luas sisi tabung = $2\pi r (r+t)$
- Luas tabung tanpa tutup = $\pi r (r+2t)$
- Volume tabung = $\pi r^2 t$
Simulasi Luas Permukaan dan Volume Tabung dengan GeoGebra
Agar lebih memahami materi tabung ini, silakan lakukan simulasi dengan
menggeser slider jari-jari dan tinggi tabung ke kanan atau ke
kiri.
D. Evaluasi
Setelah mempelajari materi tabung ini, silakan kerjakan latihan berikut
agar lebih memahami.
1. Sebuah tabung tingginya $14$ cm dan jari-jari alasnya $3$ cm. Tentukan
volume tabung tersebut.
2. Sebuah tabung terbuat dari seng dengan jari-jari $14$ cm dan tinggi
$20$ cm. Tentukan luas seng yang diperlukan untuk membuat tabung
tersebut.
3. Sebuah tempat penampungan air berbentuk tabung dengan tinggi $2$ m dan
diameter $7$ dm. Alas penampungan air itu bocor sehingga air keluar dengan
kecepatan rata-rata $5$ liter per menit. Jika air dalam tempat penampungan
tersebut penuh, air akan habis setelah berapa menit?
Demikian materi tentang tabung. Semoga bermanfaat, terima kasih
😊🙏.
Traktir saya minum kopi dengan cara memberi donasi. klik icon panah di atas. Terima kasih.

5 komentar
Untuk menyempurnakannya, yang modus text sebaiknya tetap ditulis tegak, dan bilangan dengan satuan diberi spasi (jika berkenan Pak.)
Kls:IX 'A'
IX A
image quote pre code