KERUCUT
A. Kompetensi Dasar
3.7 Membuat generalisasi luas permukaan dan volume bangun ruang sisi
lengkung (tabung, kerucut dan bola).
4.7 Menyelesaikan masalah kontekstual yang berkaitan dengan luas permukaan
dan volume bangun ruang sisi lengkung (tabung, kerucut, dan bola)
serta gabungan beberapa bangun ruang sisi lengkung.
B. Tujuan Pembelajaran (Materi Kerucut)
Setelah mempelajari materi kerucut ini, diharapkan dapat :
1. Menyebutkan unsur-unsur kerucut.
2. Menghitung luas alas, luas selimut, dan luas tutup kerucut.
3. Menghitung volume kerucut.
4. Menghitung unsur-unsur kerucut jika volume tabung diketahui.
5. Menghitung perbandingan volume kerucut karena perubahan ukuran jari-jari.
6. Menghitung besar perubahan volume kerucut, jika jari-jari berubah.
C. Materi
1. Unsur-unsur Kerucut
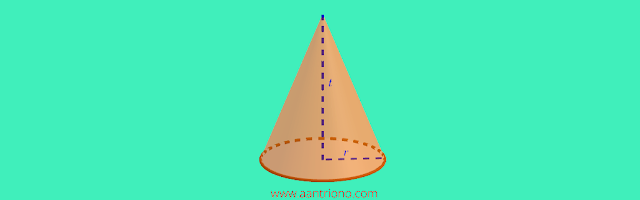
Perhatikan gambar berikut.
Gambar tersebut merupakan bangun ruang kerucut, unsur-unsurnya tampak
sebagai berikut :
- Kerucut memiliki dua sisi, yaitu sisi datar berupa bidang lingkaran berjari-jari $r$ disebut bidang alas, dan satu sisi lengkung yang disebut selimut atau sisi tegak.
- Bidang alas yang berjari-jari $r$ disebut jari-jari kerucut.
- Kerucut memiliki sebuah titik sudut sebagai puncak kerucut, jarak antara titik sudut ke titik pusat bidang alas disebut tinggi kerucut (t).
- Kerucut memiliki sebuah rusuk lengkung yang merupakan batas bidang alas dengan selimut.
2. Garis pelukis kerucut
Perhatikan gambar berikut.
Gambar tersebut menunjukkan segitiga siku-siku TOA yang bila diputar pada
$\overline{TO}$ maka akan terbentuk bangun kerucut seperti gambar berikut.
Pada gambar tersebut titik puncak kerucut (titik T) berjarak
sama terhadap titik-titik pada keliling lingkaran alas (misalnya titik
A, dan B). Dalam hal ini berarti
TA = TB = s. $\overline{TA}$, $\overline{TB}$ disebut garis pelukis
kerucut.
Jadi dari uraian tersebut dapat disimpulkan bahwa :
Garis pelukis kerucut adalah ruas garis pada selimut kerucut yang menghubungkan titik
puncak dan titik-titik pada keliling lingkaran alasnya. Garis pelukis
ditulis dengan lambang “s”.
Selanjutnya menurut teorema Pythagoras berlaku :
$s^2 = t^2 + r^2$ atau $s = \sqrt{t^2 + r^2}$
Keterangan :
s = garis pelukis
t = tinggi kerucut
r = jari-jari alas kerucut
3. Jaring-jaring Kerucut
Perhatikan gambar berikut.
Gambar tersebut menunjukkan sebuah kerucut yang bidang alasnya
berjari-jari r, dan tingginya t, berarti garis pelukis $s =
\sqrt{t^2 + r^2}$. Jika kerucut ini dipotong sepanjang garis pelukis
(s), dan sepanjang keliling sisi alasnya maka hasilnya tampak
seperti gambar berikut.
Gambar tersebut dinamakan jaring-jaring kerucut.
Dari jaring-jaring kerucut ternyata jaring-jaring ini merupakan rangkaian
bidang lingkaran berjari-jari r dan suatu bidang juring lingkaran
yang mempunyai jari-jari s, dan busur yang panjangnya $2\pi r$.
Jadi, dapat disimpulkan bahwa :
Jaring-jaring kerucut adalah rangkaian bidang lingkaran
berjari-jari r dan bidang juring lingkaran yang
mempunyai jari-jari s dan busur lingkaran yang
panjangnya $2\pi r$
4. Luas Sisi Kerucut
Perhatikan gambar berikut yang menunjukkan sebuah kerucut dengan puncak
$P$, tinggi $t$, jari-jari lingkaran alas $r$, dan garis pelukis kerucut
$s$.
Bagaimana caranya menghitung luas sisi kerucut?
Untuk mengetahui luas sisi kerucut dapat dilakukan dengan cara berikut :
- Buatlah juring lingkaran dengan pusat $120^0$ seperti tampak pada gambar di atas sebelah kanan pada suatu kertas, kemudian potong juring tersebut.
- Buatlah suatu kerucut dengan menghubungkan garis pelukis $PQ$ ke $PQ'$.
- Jiplaklah lingkaran alas kerucut yang terbentuk pada suatu kertas.
- Buka kembali kerucut dan jiplaklah tepat di atas lingkaran alas.
Jika gambarmu benar akan diperoleh gambar seperti berikut.
- Lingkaran alas dengan pusat $O$ dan jari-jari $r$.
- Selimut kerucut yang berupa juring lingkaran $PQQ'$ dengan jari-jari adalah garis pelukis selimut $s$ dan panjang busur =$2\pi r$.
Untuk mendapatkan luas juring PQQ', perhatikan uraian berikut.
Jari-jari juring $PQQ'=s$
Lingkaran dengan jari-jari $s$ mempunyai keliling = $2\pi s$ dan luas =
$\pi s^2$.
Selanjutnya diperoleh:
$\begin{aligned}
&\frac{\text{Luas juring PQQ'}}{\text{Luas lingkaran }}=\frac{\text{Panjang busur QQ'}}{\text{Keliling lingkaran}}\\
&\frac{\text{Luas juring PQQ'}}{\pi rs}=\frac{2\pi r}{2\pi s}\\
&\text{Luas juring PQQ'}=\frac{2\pi r\times \pi s^2}{2\pi s}\\
&\text{Luas juring PQQ'}=\pi rs
\end{aligned}$
Jadi, luas selimut kerucut = luas juring PQQ' = $\pi rs$
Sebagaimana telah diketahui bahwa jaring-jaring kerucut terdiri atas
selimut kerucut dan lingkaran alas sehingga luas sisi kerucut dapat
dirumuskan sebagai berikut.
$\begin{aligned} \text{Luas sisi kerucut}& =\text{luas selimut kerucut + luas lingkaran alas}\\
&=\pi rs + \pi r^2\\
&=\pi r(r + s)
\end{aligned}$
Luas selimut kerucut = $\pi rs$, dan Luas sisi kerucut = $\pi r (r+s)$
Contoh soal :
1. Sebuah kerucut mempunyai panjang jari-jari alasnya $6$ cm dan
tingginya $8$ cm. Hitunglah luas sisi kerucut tersebut $(\pi = 3,
14)$
2. Hitunglah luas sisi kerucut yang jari-jarinya $7$ cm dan garis
pelukisnya $14$ cm.
Penyelesaian :
1. Jari-jari alas = $r=6$ cm
Tinggi kerucut = $t=8$ cm
Panjang garis pelukisnya adalah :
$\begin{aligned}
s^2&=r^2+t^2\\
s^2&=6^2+8^2\\
s^2&=36+64\\
s&=\sqrt{100}\\
s&=10
\end{aligned}$
$\begin{aligned}
\text{Luas sisi kerucut}& = \pi r(r+s)\\
&=3,14\times 6\times (6+10)\\
&=3,14\times 6\times 16\\
&=301,44
\end{aligned}$
Jadi, luas sisi kerucut adalah $301,44\ cm^2$
2. Jari-jari alas = $7$ cm
Garis pelukis = $14$ cm
$\begin{aligned} \text{Luas sisi kerucut}& = \pi r(r+s)\\ &=\frac{22}{7}\times 7\times(7+14)\\ &=22\times 21\\ &=462 \end{aligned}$
Jadi, luas sisi kerucut adalah $462\ cm^2$
5. Volume Kerucut
Perhatikan gambar berikut.
Gambar tersebut menunjukkan bangun limas segi banyak beraturan, yaitu
limas yang yang alasnya berbentuk segi banyak dan beraturan. sebuah
kerucut dapat dipandang sebagai limas segi banyak beraturan yang rusuk
alasnya diperbanyak sampai membentuk lingkaran seperti gambar
berikut.
$\text{Volume kerucut} = \frac{1}{3}\times\text{luas
alas}\times\text{tinggi}$. Karena alas kerucut berbentuk lingkaran maka
luas alasnya adalah luas lingkaran. Dengan demikian, volume kerucut dapat
dirumuskan sebagai berikut.
$V = \frac{1}{3}\times \pi r^2t$
Keterangan :
V = volume kerucut
r = jari-jari lingkaran alas
t = tinggi kerucut
Karena $r = \frac{1}{2}d$, dengan d adalah diameter lingkaran maka
bentuk lain rumus volume kerucut adalah sebagai berikut.
$\begin{aligned} V&=\frac{1}{3}\pi rt\\ &=\frac{1}{3}\pi (\frac{1}{2}d)^2t\\ &=\frac{1}{3}\pi \frac{1}{4}d^2t\\ &=\frac{1}{12}\pi d^2t \end{aligned}$
Volume kerucut = $\frac{1}{12}\pi d^2t$
1. Sebuah kerucut mempunyai jari-jari $9$ cm dan tinggi $4$ cm. Hitunglah
volume kerucut tersebut.
2. Diketahui volume sebuah kerucut adalah $314\ cm^3$. Jika jari-jari
alasnya $5$ cm, tentukan panjang garis pelukisnya.
3. Perhatikan gambar berikut.
Penyelesaian.
$\begin{aligned}1.\ \text{Volume kerucut}& = \dfrac{1}{3}\times \text{luas\ alas}\times \text{tinggi}\\
&=\dfrac{1}{3}\times \pi \times r^\times t\\
&=\dfrac{1}{3}\times 3,1\times 9\times \\
&=339,12 \end{aligned}$
Contoh.
Cara mengerjakan evaluasi :
1. Berdo'a terlebih dulu sebelum mengerjakan soal.
Demikian materi tentang Kerucut. Jika ada kritik, saran ataupun masukan silakan tulis di kolom komentar. Semoga bermanfaat, terima kasih 😊🙏.
Jadi, volume kerucut adalah $339,12\ cm^3$
$. \begin{aligned} 2.\
V&=\frac{1}{3}\pi r^2t\\
314&=\frac{1}{3}\times 3,14\times5^2\times t\\
t&=12\\
\end{aligned}\\
\text{Misalkan panjang garis pelukis =s, maka} :\\
\begin{aligned}
s&=\sqrt{r^2+t^2}\\
&=\sqrt{5^2+12^2}\\
&=\sqrt{25+144}\\
&=\sqrt{169}\\
&=13
\end{aligned}$
Jadi, panjang garis pelukisnya adalah $13$ cm.
$\begin{aligned}
3.\ V_{\text{tabung}}&=\pi r^2t\\
&=\frac{22}{7}\times 7\times 7\times 10\\
&=1.540 \\
V_{\text{kerucut}}&=\frac{1}{3}\pi r^2t\\
&=\frac{1}{3}\times \frac{22}{7}\times 7\times 7\times 9\\
&=462 \\
\end{aligned}$
Jadi, volume bangun tersebut adalah :
Volume tabung + Volume kerucut = $1.540\ cm^3 + 462\ cm^3 = 2.002\ cm^3$
6. Menghitung Perbandingan Volume Kerucut Karena Perubahan Jari-Jari
Suatu kerucut semula alasnya berjari-jari r, tinggi t, dan volume v, bila jari-jari mengalami penambahan atau pengurangan
a satuan, diperoleh perbandingan : $V : V_{\text{baru}} = r^2 :
(r+a)^2$. Jika jari-jari mengalami perubahan k kali, diperoleh
perbandingan : $V : V_{\text{baru}} = r^2 : (rk)^2 = 1 : k^2$
Contoh.
1.Suatu kerucut dengan jari-jari $2$ cm dan tinggi $6$ cm. Tentukan :
a. Perbandingan sebelum dan sesudah mengalami penambahan jari-jari $1$
cm.
b. Perbandingan volume sebelum dan sesudah mengalami perubahan $3$ kali
jari-jari semula.
2. Suatu kerucut jari-jari alasnya $7$ cm dan tingginya $10$ cm. Tentukan
perubahan volume kerucut, jika :
a. Jari-jari berkurang $2$ cm
b. Jari-jari berubah $\frac{1}{2}$ kali
c. jari-jaridan tinggi berubah $\frac{1}{2}$
d. Jari-jari bertambah $1$ cm dan tinggi berkurang $2$ cm.
Penyelesaian.
$\begin{aligned} 1.a\
V : V_{\text{baru}}&=r^2:(r+a)^2\\
&=2^2:(2+1)^2\\
&=2^2:3^2 \\
&=4:9
\end{aligned}$
$\begin{aligned}
b.\ V : V_{\text{baru}}&=1:(k)^2\\
&=1:(3)^2\\
&=1:9 \\
\end{aligned}$
$\begin{aligned}
2.\ V_{\text{semula}}&=\frac{1}{3}\pi r^2t\\
&=\frac{1}{3}\times 3,14\times 7^2\times 10\\
&=512,87
\end{aligned}$
Jadi, volume kerucut mula-mula adalah $512,87\ cm^3$
a. Jari-jari baru = $7-2=5$
$\begin{aligned}
V_{\text{baru}}&=\frac{1}{3}\pi r^2_{\text{baru}}t\\
&=\frac{1}{3}\times 3,14\times 5^2\times 10\\
&=261,67
\end{aligned}$
Jadi, jika jari-jari berkurang $2$ cm, maka volume menjadi $261,67\ cm^3$
atau terjadi pengurangan volume $251,20\ cm^3$.
b. Jari-jari baru = $\frac{1}{2}r=\frac{1}{2}(7)=3,5$
$\begin{aligned}
V_{\text{baru}}&=\frac{1}{3}\pi r^2_{\text{baru}}t\\
&=\frac{1}{3}\times 3,14\times (3,5)^2\times 10\\
&=128,216
\end{aligned}$
Jadi, jika jari-jari berubah $\frac{1}{2}$ kali, maka volume menjadi
$128,216\ cm^3$ atau berubah $\frac{1}{4}$ kalinya.
c. Jari-jari baru = $\frac{1}{2}r=\frac{1}{2}(7)=3,5$
Tinggi baru = $\frac{1}{2}t=\frac{1}{2}\times
10=5\ cm$
$\begin{aligned}
V_{\text{baru}}&=\frac{1}{3}\pi r^2_{\text{baru}}t_{\text{baru}}\\
&=\frac{1}{3}\times 3,14\times (3,5)^2\times 5\\
&=320,54
\end{aligned}$
Jadi, jika jari-jari berubah $\frac{1}{2}$ kali dan tinggi berubah
$\frac{1}{2}$ kali, maka volume menjadi $320,54\ cm^3$. Berarti, volume
berkurang $192,33\ cm^3$
d. Jari-jari baru = $r=7+1=8$
Tinggi baru = $10-2=8$
$\begin{aligned}
V_{\text{baru}}&=\frac{1}{3}\pi r^2_{\text{baru}}t_{\text{baru}}\\
&=\frac{1}{3}\times 3,14\times (8)^2\times 8\\
&=558,08
\end{aligned}$
Jadi, jika jari-jari bertambah $1$ cm dan tinggi berkurang $2$ cm, maka
volumenya menjadi $558,08\ cm^3$ atau volume bertambah $45,21\ cm^3$.
7. Simulasi GeoGebra
Agar lebih memahami materi kerucut ini, silakan lakukan simulasi dengan
menggeser slider jari-jari dan tinggi kerucut ke kanan atau ke kiri.
D. Evaluasi
Setelah selesai mempelajari materi kerucut, dan untuk mengukur pemahaman
tentang materi tersebut, silakan kerjakan evaluasi berikut ini.Cara mengerjakan evaluasi :
1. Berdo'a terlebih dulu sebelum mengerjakan soal.
2. Tulis nama dan kelas pada tempat yang disediakan.
3. Pilih dan klik jawaban yang benar pada opsi A, B, C, atau D.
4. Setelah selesai mengerjakan gulir ke bawah dan klik finish.
5. Klik Check my answers.
6. Screenshot nilai yang keluar dan kirim hasil screenshot ke guru kalian.
3. Pilih dan klik jawaban yang benar pada opsi A, B, C, atau D.
4. Setelah selesai mengerjakan gulir ke bawah dan klik finish.
5. Klik Check my answers.
6. Screenshot nilai yang keluar dan kirim hasil screenshot ke guru kalian.
7. Jika nilai belum mencapai 70 agar mengulang mengerjakan soal tersebut,
karena KKM adalah 70.
8. Selamat mengerjakan, sukses selalu.
Mathematics Interactive Worksheet, an interactive worksheet by
aantriono
liveworksheets.com
liveworksheets.com
Silakan dilihat video panduan berikut untuk mengerjakan soal evaluasi
tersebut.
Demikian materi tentang Kerucut. Jika ada kritik, saran ataupun masukan silakan tulis di kolom komentar. Semoga bermanfaat, terima kasih 😊🙏.
Traktir saya minum kopi dengan cara memberi donasi. klik icon panah di atas. Terima kasih.









1 komentar
image quote pre code